Algorithms
Preprocessed Cumulative Reconstructor with domain decomposition (P-CuReD)
The direct imaging of extra-solar planets is one of the most challenging fields in modern astronomy because of the huge contrast between the brightness of the hosting star and of the orbiting planet. For high-contrast imaging at very small angular separations, dedicated exoplanet finding instruments are currently under development for ELTs, e.g., EPICS on the European ELT (E-ELT). Such instruments will include an eXtreme Adaptive Optics (XAO) system, which is a Single Conjugate AO (SCAO) system with a huge number (10^4 − 10^5 ) of actuators which need to be controlled at a frequency of about 3 kHz.

Preprocessed Cumulative Reconstructor with domain decomposition (P-CuReD) is a fast algorithm for wavefront reconstruction developed for extreme / single conjugate adaptive optics systems on a 42m telescope. Namely, we considered an XAO system on a 42 m telescope equipped with a pyramid wavefront sensor with 200x200 subapertures. It was assumed that the pyramid sensor can be modulated in a circular or linear manner, or has no modulation.

We analyzed theoretically the forward operators describing the relationship between the incoming phase screen and the pyramid sensor data. To reconstruct the wavefront, one has to invert the sensor operators, which are rather complicated non-linear singular integral operators. To simplify the problem of wavefront reconstruction, we adopted several assumptions which allow to linearize the forward operators.
Further, we have studied theoretically the relation between data from the linearized pyramid and Shack-Hartmann wavefront sensors. From this research, a wavefront reconstruction algorithm called Preprocessed Cumulative Reconstructor with Domain decomposition (P-CuReD) has originated. The algorithm consists of two consecutive steps - a data preprocessing, and an application of the CuReD algorithm, which is a very fast algorithm for wavefront reconstruction from Shack-Hartmann sensor data.
The data preprocessing step is derived from the theoretical relationship between the two sensors in the Fourier domain. However, the data preprocessing is performed on the space domain, which allows to avoid the application of the time consuming Fourier transforms. The data preprocessing step consists in a row-wise and column-wise convolution of the sensor data with a one-dimensional kernel. The convolution kernels for various modulation scenario have been derived theoretically as well as numerically. The discretized kernels are rather sparse and therefore, the convolution is very cheap.
The P-CuReD method was tested in closed loop simulations run on the ESO simulation tool OCTOPUS. For a set of various atmospheric conditions and various photon flux cases, the simulation results confirm that in terms of the AO correction quality, the P-CuReD algorithm is comparable to the standard MVM approach. In the low flux regimes the P-CuReD method provides a better quality, due to the smoothing properties of the data preprocessing step and good noise propagation properties of the CuReD algorithm. The P-CuReD has an additional advantage: in contrast to the MVM, our method has no parameters which need to be optimized when the seeing conditions change.

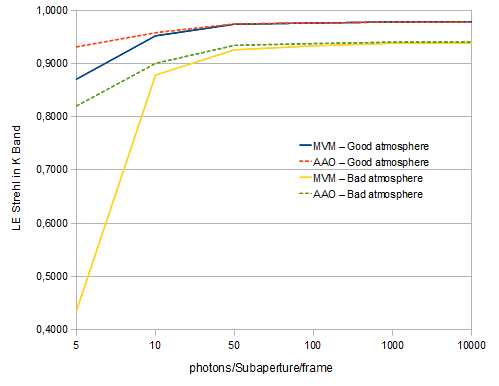

The greatest advantage of our algorithm is the reconstruction speed - the P-CuReD method is significantly faster than MVM. The algorithm has linear complexity O(n), where n is the number of subapertures, and is to a large extent parallelizable and pipelinable. To demonstrate the improvement in the computing time, the RTC prototypes of both methods, the P-CuReD and the MVM, were run on several computing systems. Depending on the configuration of the machine, we achieve the speedup factors of 800 to 1100.

References
[2] A. Neubauer. On the ill-posedness and convergence of the Shack-Hartmann based wavefront reconstruction. J. Inv. Ill-Posed Problems, 18:551-576, 2010.
[4] M. Zhariy, A. Neubauer, M. Rosensteiner, and R. Ramlau. Cumulative wavefront reconstructor for the Shack-Hartman sensor. Inverse Problems and Imaging, 5(4):893-913, Nov 2011.
[6] A. Neubauer. A new cumulative wavefront reconstructor for the Shack-Hartmann sensor. J. Inv. Ill-Posed Problems, 21:451-476, 2013.
Conference Proceedings
Conference Talks
Posters


